Resumen: Este capítulo estudia los mecanismos físicos mediante los cuales se producen los sonidos armónicos o musicales. Tomando como paradigma el caso de una cuerda tensada y fija en sus extremos, muestra que los sonidos musicales son el resultado de ondas estacionarias unidimensionales que dan lugar a modos de resonancia armónicos, es decir, múltiplos enteros de una frecuencia fundamental. Los vídeos elaborados con Matlab que simulan la cuerda de un instrumento musical sirven para ilustrar cómo se producen las ondas estacionarias y cómo surge el fenómeno de la resonancia.
Introducción
El material de la música, el sonido armónico, es un fenómeno tan frecuente que forma parte de nuestra experiencia cotidiana en el reconocimiento del entorno. En efecto, el sonido armónico está por todas partes: si ponemos un poco de atención, podemos oír notas musicales en medio del ruido del tráfico, en el silbido del aire cuando se filtra por los tubos de una chimenea o por las grietas de las rocas, en el canto de los pájaros o incluso en el aullido de algunas fieras. Por otra parte, es sencillo generar sonidos armónicos: basta soplar ligeramente en el cuello de una botella vacía, frotar con suavidad el borde de una copa de cristal o pellizcar una cuerda lo suficientemente tensa para que se produzcan sonidos musicales.
La pregunta es: ¿por qué es tan habitual la existencia de vibraciones cuyos componentes tienen frecuencias que son múltiplos enteros de una frecuencia fundamental? La respuesta nos lleva a la geometría: si el sonido armónico abunda tanto en la naturaleza y en los utensilios de todo tipo que hemos fabricado los humanos es porque es muy común la existencia de estructuras geométricas adecuadas para la generación de ondas estacionarias armónicas y para su amplificación mediante resonancias.
En cierto modo podemos decir que todo sonido armónico se produce mediante un proceso de resonancia, un proceso por el cual la onda excitadora se acopla con sus sucesivos reflejos, dando lugar a la aparición de ondas estacionarias. A lo largo de este capítulo vamos a examinar por qué se produce el sonido armónico. Para ello estudiaremos el mecanismo físico mediante el cual surgen las ondas estacionarias y el fenómeno de la resonancia. Comprenderemos que determinadas propiedades físicas y geométricas de los cuerpos que vibran posibilitan la aparición de ondas estacionarias con unos modos de resonancia que son armónicos entre sí y que cuando estos modos naturales de vibración son excitados por algún agente surgen sonidos armónicos.
Mediante vídeos ilustrativos que he elaborado con Matlab y que simulan el comportamiento de una cuerda tensada y fija en sus extremos, podremos experimentar qué son las ondas estacionarias y en qué consiste el fenómeno de la resonancia. Los vídeos nos van a permitir observar cómo las ondas estacionarias surgen de la interferencia reiterada de una onda sinusoidal con su reflejo. Veremos también que la cuerda tensada, como todo sistema vibratorio unidimensional, posee por naturaleza unos modos de vibración que son armónicos. Observaremos que la resonancia se produce cuando un sistema vibratorio es excitado por cualquier perturbación, por pequeña que sea, que coincida con una de sus frecuencias naturales de vibración. Y comprenderemos por qué, al ponerse a vibrar en las frecuencias de estos modos naturales de vibración, la cuerda produce un sonido periódico y musical.
Finalmente, antes de entrar en materia, me gustaría señalar que el fenómeno de la resonancia no sólo es importante para la acústica musical, sino que atañe a toda la acústica e incluso a la física en su conjunto y, de una u otra manera, a la ciencia en general. La noción de resonancia ha salido del campo estrictamente acústico y ha servido para explicar multitud de fenómenos en todas las áreas de las ciencias, desde fenómenos electromagnéticos hasta los que conciernen a la física de partículas, a la astronomía, e incluso a la biología molecular. Allí donde está presente la vibración o la oscilación está también presente el fenómeno de la resonancia.
La cuerda como paradigma de un sistema vibratorio unidimensional
Para estudiar los fenómenos de las ondas estacionarias y de la resonancia vamos a analizar lo que ocurre en una simple cuerda tensada y fija en sus extremos. Este modelo puede ser considerado como paradigma de un sistema vibratorio unidimensional. Dado que los sonidos musicales suelen ser producidos por sistemas vibratorios unidimensionales, si analizamos el comportamiento de una cuerda cuando es inducida a vibrar podremos comprender los mecanismos mediante los cuales se produce el sonido armónico.
En todo movimiento ondulatorio hay que distinguir entre el movimiento de propagación de la onda y el movimiento oscilatorio que realiza cada una de las partículas que se ven afectadas por el paso de la onda. Cuando la dirección de ambos movimientos es la misma, decimos que las ondas son longitudinales, como vimos que ocurre con las condensaciones y rarefacciones en el aire al transmitir un sonido. Cuando la dirección del movimiento oscilatorio es perpendicular a la del movimiento propagatorio, decimos que las ondas son transversales.
Por otra parte, la propagación de las ondas puede producirse en las tres dimensiones del espacio, en dos dimensiones o solamente en una: las condensaciones y rarefacciones que se producen al propagarse un sonido por el aire en un espacio abierto son de carácter tridimensional, pues se extienden de forma radial por todo el espacio circundante; la ondulación que se propaga por las aguas de un estanque o por la membrana de un tambor es bidimensional, pues viaja a lo largo y ancho de una superficie; y las perturbaciones que se propagan a través de una cuerda tensada o en el aire contenido en el tubo de una flauta son unidimensionales, pues viajan en una sola dirección del espacio.
Al margen de que sean transversales o longitudinales, los sistemas vibratorios unidimensionales tienden a producir ondas estacionarias con modos normales de vibración armónicos. Por eso los sonidos musicales son generados por sistemas vibratorios unidimensionales, tales como los instrumentos de cuerda y los de viento. Habitualmente las cuerdas de los instrumentos al excitarse dan lugar a ondas transversales: el macillo en un piano golpea la cuerda y la desplaza transversalmente; lo mismo sucede al ser frotada la cuerda de un violín con un arco o al ser pulsada la cuerda de una guitarra con el dedo. En el caso de los instrumentos de viento, sin embargo, las ondas que se producen son longitudinales, pues la oscilación de las partículas de aire se produce en la misma dirección en la que se propagan las variaciones de la presión, es decir, a lo largo de la propia longitud de la masa de aire que está contenida en el tubo.
Para estudiar cómo se genera el sonido armónico me ha parecido oportuno tomar como ejemplo un sistema constituido por una cuerda tensada que está fija en ambos extremos, como puede ser la cuerda de un piano, de una guitarra o de cualquier otro instrumento similar. Se trata de un sistema vibratorio unidimensional y transversal. Dado que en las ondas transversales las partículas oscilan de forma perpendicular a la dirección de propagación, son más fáciles de observar que las ondas longitudinales, donde la oscilación de las partículas tiende a camuflarse con el movimiento de la onda que propaga la perturbación. Aunque al estudiar el comportamiento de la cuerda tensada nos centraremos en las ondas transversales, las ideas que vamos a examinar pueden ser generalizadas al caso de las ondas longitudinales unidimensionales, como las que se producen en el interior de los tubos de los instrumentos de viento.
Así pues, con el propósito de permitir entender con facilidad cómo se producen las ondas estacionarias y en qué consiste el fenómeno de la resonancia, he fabricado varios vídeos en los que se simula a cámara lenta el movimiento de una cuerda cuando se provocan en ella diversas perturbaciones transversales. Supondremos que se trata de una cuerda de piano sin encorchar de un metro de longitud —como podría ser cualquiera de las cuerdas que dan una nota en la octava que va de do3 a do4— y que ha sido extraída del instrumento y sujetada por sus extremos a unos soportes que la mantienen tensada. Supondremos también que estos soportes pueden ser desplazados arriba y abajo mediante algún artilugio mecánico para inducir en la cuerda diversos tipos de perturbaciones. La perturbación se provocará mediante el desplazamiento vertical del soporte izquierdo al que está unida la cuerda o, en alguna ocasión, de los dos soportes. Una vez que la perturbación haya sido introducida, los soportes volverán a quedar fijos. A fin de modelizar la inercia y la elasticidad, podemos considerar que la cuerda está constituida por un conjunto de bolitas unidas por pequeñas gomas o muellecillos que se estiran y se encogen.
En el eje vertical de la gráfica que aparecen en los vídeos se representa el desplazamiento vertical de las partículas que suponemos forman la cuerda. Como nos interesa observar el detalle de la perturbación y de sus reflejos e interferencias, las unidades del eje vertical están en milímetros. En el eje horizontal se representan las sucesivas posiciones de la cuerda a lo largo de su longitud. Las unidades en este caso, sin embargo, están en metros. Esta diferencia en las unidades hace que en los vídeos resulten muy exageradas las deformaciones de la cuerda provocadas por su vibración (tengamos en cuenta que la cuerda real mide un metro y que la deformación máxima que va a sufrir es de dos milímetros), pero nos va a permitir ver con mucha más facilidad los fenómenos ondulatorios que se producen.
Por otra parte, como queremos observar con detenimiento el movimiento que se genera en la cuerda, nos interesa que en nuestra simulación la velocidad de propagación de las perturbaciones sea suficientemente lenta. La velocidad con la que se transmite cualquier perturbación transversal en una cuerda real está determinada por la tensión a la que está sometida y por la masa por unidad de longitud que posee. En el caso de una cuerda de piano que emite una nota media (como puede ser el la3) la velocidad de propagación de una perturbación transversal puede estar en torno a los 400 m/s. En nuestra simulación, sin embargo, la velocidad con la que se propaga la perturbación a lo largo de la cuerda es de 1 metro por segundo, es decir, 400 veces más lenta que en la cuerda real. El movimiento vertical del soporte mediante el que se generan las perturbaciones está ralentizado en esa misma proporción.
Hay que tener en cuenta también que la cuerda de nuestro modelo se comporta de forma ideal. En las simulaciones de los vídeos se ha prescindido del rozamiento con el aire o con los soportes que la sujetan, por lo que no se produce ninguna amortiguación en el movimiento de la cuerda. Así mismo, supondremos que la cuerda vibra siempre en el mismo plano —en concreto, en el plano vertical arriba/abajo—, aunque las cuerdas de los instrumentos reales no se comportan siempre así (por ejemplo, en un piano de cola, como consecuencia de la acción del macillo que la golpea desde abajo, la cuerda comienza a oscilar en la dirección arriba/abajo, pero durante su vibración tiende a rotar su plano de oscilación y a oscilar también de izquierda a derecha, en la dirección paralela al teclado).
Comenzaremos examinando cómo se propaga por la cuerda una perturbación transversal y cómo esa perturbación se refleja cuando llega a los extremos fijos. Luego analizaremos lo que ocurre cuando interfieren dos perturbaciones que viajan en sentidos opuestos. Después comprobaremos que las ondas estacionarias surgen de la interferencia de una onda sinusoidal con su reflejo, cuando, en el tiempo que tarda una oscilación en completarse, la onda recorre exactamente una parte entera del camino de ida y vuelta a lo largo de la cuerda. A continuación veremos que la cuerda tensada, en función de la velocidad de propagación ondulatoria, posee unos modos normales de vibración propios, cuyas frecuencias siguen la serie armónica. Después podremos observar que, cuando una cuerda es excitada en cualquiera de esos modos de resonancia naturales, basta una mínima perturbación para producir una gran ondulación. Y finalmente, podremos ver el movimiento de una cuerda cuando resuena simultáneamente en varios de sus modos naturales de vibración, como sucede habitualmente en las cuerdas de los instrumentos musicales.
Propagación y reflexión de una perturbación transversal sobre una cuerda
Para estudiar cómo se propaga una perturbación transversal a lo largo de una cuerda y cómo se refleja al llegar a un punto fijo que le impide seguir en el mismo sentido, he fabricado un vídeo en el que se simula el comportamiento de nuestra cuerda cuando se introduce en ella una perturbación de 1,5 milésimas de segundo de duración. Imaginemos que para iniciar la perturbación hemos desplazado, con ayuda de un artilugio mecánico, 1 mm hacia arriba el soporte al que está sujeta la cuerda por la izquierda y luego lo hemos hecho descender hasta su posición original. Dado que la simulación está ralentizada 400 veces, la duración del impulso en el vídeo de nuestra simulación es de 0,6 segundos. Los 20 segundos que dura el vídeo corresponden a las primeras 50 milésimas de segundo del movimiento de la supuesta cuerda real.
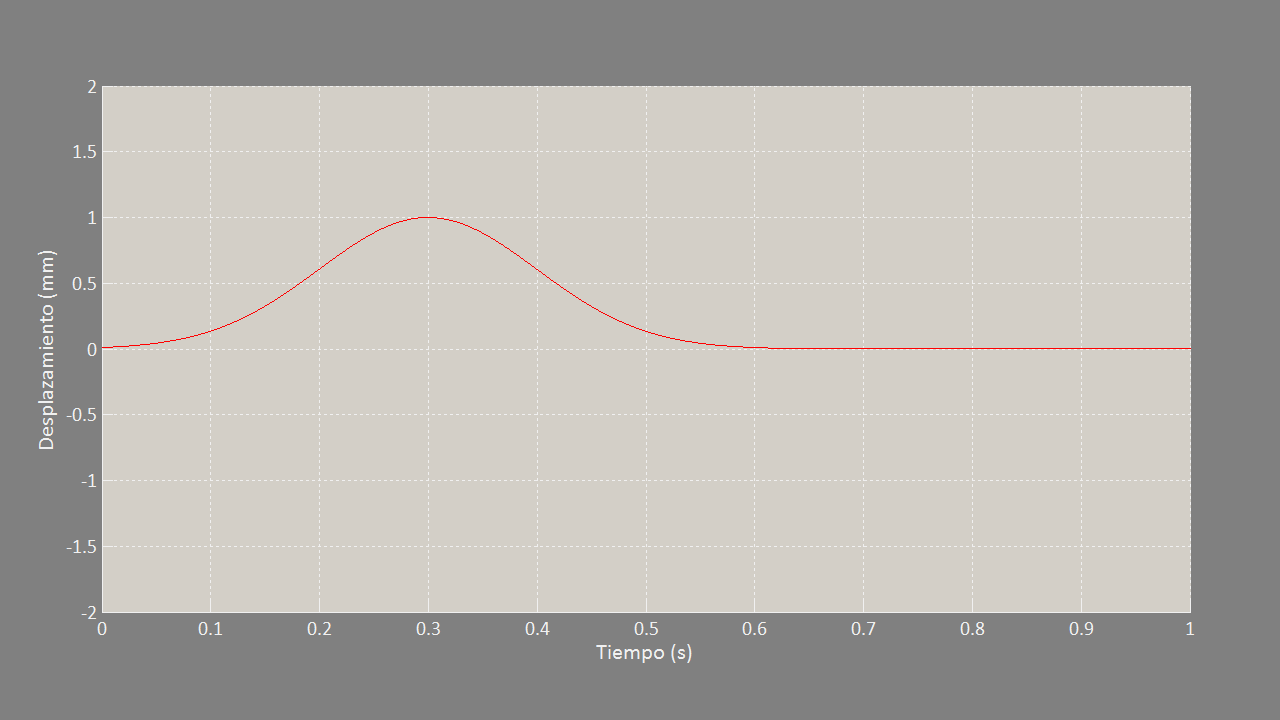
Para que se apreciara claramente en el vídeo que la perturbación se invierte cuando se refleja en los soportes fijos de los extremos, interesaba que el impulso inicial fuera sólo hacia arriba, sin que al descender sobrepasara la posición de equilibrio de la cuerda, de manera que antes de reflejarse por primera vez la perturbación viajara sólo por la parte superior. Para ver cómo es el impulso que ha generado la perturbación, es decir, el movimiento vertical que ha realizado el soporte de la cuerda, presento una gráfica que muestra el desplazamiento del soporte en función del tiempo.
Podemos apreciar que el desplazamiento del soporte es simétrico y que tiene forma de campana de Gauss. Las unidades del eje horizontal corresponden al tiempo de la simulación en el vídeo.
Veamos ahora el vídeo que simula el comportamiento de la cuerda.
Podemos observar en el vídeo que el movimiento vertical del soporte izquierdo provoca una perturbación en la cuerda que se transmite a lo largo de ella por la parte superior hasta alcanzar el soporte derecho. Allí la perturbación, al no poder continuar, se refleja de modo invertido, regresando por la parte inferior hasta alcanzar el soporte izquierdo, donde se vuelve a reflejar para invertirse de nuevo y seguir por la parte superior. Dado que no hemos contemplado ningún tipo de amortiguación, la propagación de la perturbación se repite constantemente, reflejándose de modo invertido cada vez que alcanza un extremo.
La propagación de la perturbación es consecuencia de la elasticidad de la cuerda. En nuestra simulación podemos apreciar que la elasticidad introduce un retraso en la comunicación del movimiento de una bolita a la siguiente, de modo que las bolitas van repitiendo sucesivamente, pero con su correspondiente demora, el desplazamiento vertical del impulso inicial, como podemos apreciar en el vídeo si atendemos al movimiento individual de cualquiera de ellas. De esta manera el movimiento temporal que ha realizado el soporte, la campana de Gauss que hemos visto en la figura 1, queda dibujado en el espacio. Así mismo, la anchura de la perturbación que dibuja la cuerda depende también de los retrasos que introduce la elasticidad, los cuales determinan la velocidad con la que se propaga cualquier perturbación a lo largo de esa cuerda. En la simulación ralentizada de nuestro vídeo, dado que la velocidad de transmisión es de 1 m/s y que el impulso dura 0,6 segundos, la anchura de la deformación provocada en la cuerda es de 0,6 metros.
La reflexión se produce cuando la perturbación que se transmite a lo largo de la cuerda encuentra un obstáculo que no puede mover. En nuestro caso, cuando la perturbación llega al extremo derecho de la cuerda no puede desplazar el soporte. Puesto que, según la Tercera Ley de Newton, la fuerza ejercida hacia arriba por la cuerda sobre el soporte es la misma que la que el soporte ejerce hacia abajo sobre la cuerda, el resultado es que el soporte, al no poder moverse, hace que la cuerda rebote hacia abajo, con lo que la perturbación se invierte y retorna por la parte inferior. La misma situación se repite cuando la cuerda llega de nuevo al soporte izquierdo, el cual, una vez introducido el impulso inicial, ha quedado también fijo. De nuevo la perturbación rebota y sigue su recorrido, ahora por la franja superior.
Podemos también interpretar el fenómeno de la reflexión como el resultado de la superposición de dos perturbaciones simétricas que viajaran en sentido opuesto a lo largo de dos cuerdas virtuales. Esta forma de entenderlo es más intuitiva y nos sirve para explicar los desplazamientos que sufre la cuerda en los momentos en los que se solapa la perturbación incidente y la reflejada, lo cual nos va a facilitar el estudio de las ondas estacionarias.
Estas dos cuerdas virtuales, que no estarían sujetas a ningún soporte, se prolongarían por un espacio imaginario que existiría más allá del obstáculo fijo en el que se refleja la perturbación real. La prolongación sería igual a lo que mide la cuerda real, por lo que las cuerdas imaginarias medirían el doble de ésta. Por una de estas cuerdas imaginarias viajaría la perturbación incidente, que se prolongaría por el espacio imaginario sin ser influida por la existencia del obstáculo; por la otra viajaría en sentido opuesto la perturbación reflejada, una perturbación idéntica a la real, pero invertida, que se habría originado simultánea y simétricamente en esta segunda cuerda imaginaria. En todo momento el desplazamiento de cada punto de la cuerda real sería el resultado de la superposición lineal de ambas cuerdas virtuales.
Entenderemos mejor esta idea si imaginamos que en el punto del espacio en el que se halla el obstáculo que la perturbación no puede mover —en nuestro caso, el soporte derecho al que está fijada la cuerda— existiera una suerte de espejo que separara el espacio real del espacio virtual. Veamos un vídeo de carácter didáctico en el que se ilustra lo que ocurre cuando la misma perturbación del vídeo anterior se refleja en el soporte derecho. Para poder apreciar los detalles, la velocidad del vídeo ha sido ralentizada 5 veces respecto al anterior.
En el vídeo de la figura 3 podemos ver dos planos claramente diferenciados y separados por una línea blanca vertical que representa el espejo. A la izquierda aparece el plano de la realidad, cuyo fondo está en color azul oscuro, el mismo color que el del resto de los vídeos que simulan el comportamiento de la cuerda, y a la derecha está el plano virtual, el del otro lado del espejo, en color gris.
La cuerda está representada en el mundo de la realidad por las mismas bolitas y gomillas que en el vídeo anterior. Las dimensiones coinciden: la longitud es de 1 metro y la anchura de la perturbación es de 0,6 metros. Junto a la cuerda, por encima y por debajo, vemos unas líneas de puntos que representan las cuerdas imaginarias por donde viajan las perturbaciones virtuales. Ambas líneas deberían coincidir exactamente con la cuerda, pero, para que resultara más fácil distinguirlas, las he dibujado ligeramente por encima y por debajo de la cuerda real. Por la línea de arriba, en color amarillo, va la perturbación incidente, la que va de la realidad al espejo, la cual continúa su camino cuando se encuentra con el soporte fijo, como si no hubiera obstáculo alguno. Por la línea de abajo, en color turquesa, viaja la perturbación reflejada, la originada al otro lado del espejo y que se dirige al plano de la realidad.
Observamos que, a la vez que se introduce una perturbación que afecta a la cuerda real de nuestra simulación y a la línea de puntos amarilla, al otro lado del espejo se inicia la misma perturbación, pero invertida, una perturbación que viaja por la línea de puntos de color turquesa con la misma velocidad que la perturbación original. Vemos que ambas perturbaciones siguen por su línea de puntos como si no hubiera ningún obstáculo, atravesando en el mismo instante la separación entre la realidad y el mundo del espejo.
Vemos que la cuerda real, la que está formada por las bolitas, se comporta como si fuera el resultado de sumar los desplazamientos de ambas perturbaciones virtuales, la que va por la línea de puntos amarilla y la que va por la línea de puntos turquesa. Esto es de especial interés para explicar lo que sucede en el tiempo en el que la perturbación incidente y la reflejada se solapan. Podemos apreciar que ambas perturbaciones, la incidente y la reflejada, alcanzan a la vez el soporte fijo de la cuerda, es decir, la frontera entre el mundo imaginario y el real, y a partir de ese momento empiezan a solaparse hasta que cada una termina de pasar totalmente al otro lado. Esto ocurre porque ambas perturbaciones han sido producidas simultáneamente a la misma distancia del punto del reflejo y viajan a la misma velocidad. Así mismo, puesto que una es la inversa de la otra, el valor de su superposición en el punto en el que se produce el reflejo (es decir, el valor de la suma de sus desplazamientos individuales en el extremos fijo de la cuerda real) como era de esperar, es siempre cero.
Superposición de dos perturbaciones que viajan en sentido opuesto sobre una cuerda
Examinaremos a continuación el comportamiento de la cuerda cuando se cruzan en ella dos perturbaciones que se desplazan en sentidos opuestos. He fabricado dos vídeos en los que podemos ver que cuando las dos perturbaciones se solapan, sus desplazamientos se suman, pero que, una vez han terminado de cruzarse, cada una de ellas continúa su camino sin sufrir ninguna modificación, como si no hubiera ocurrido nada.
En ambos vídeos las perturbaciones han sido ocasionadas por dos impulsos dados simultáneamente en los dos extremos de la cuerda mediante el desplazamiento vertical de los respectivos soportes. En el primer vídeo (el de la figura 4 y su repetición a cámara lenta en la figura 5) los dos impulsos desplazan la cuerda hacia arriba, mientras que en el segundo vídeo (el de la figura 6) el impulso de la izquierda la desplaza hacia arriba y el impulso de la derecha la desplaza hacia abajo. Por ello, en el primer caso las dos perturbaciones interfieren constructivamente, mientras que en el segundo lo hacen destructivamente. Los impulsos son similares a los que hemos visto en el vídeo anterior, es decir, tienen forma de campana de Gauss, y en la simulación ralentizada del vídeo también duran 0,6 segundos. La duración de los dos vídeos es de 20 segundos, y corresponden a las primeras 50 milésimas de segundo del movimiento de la cuerda real. Para facilitar la distinción de cada una de las perturbaciones, ahora la amplitud de cada uno de los impulsos es diferente: mientras el impulso izquierdo es de 1 mm, la del derecho es de 0,7 mm.
Empezaremos observando cómo se producen las interferencias constructivas.
En el vídeo de la figura 4 podemos ver que las perturbaciones provocadas en la cuerda por el desplazamiento hacia arriba de ambos soportes viajan por la parte superior en sentidos opuestos, se superponen cuando se cruzan, continúan su camino sin alterarse y se reflejan al llegar a los extremos fijos, viajando entonces ambas por la parte de abajo. Para apreciar con detalle lo que sucede es necesario reconocer primero cada una de las dos perturbaciones por separado. Puede servirnos de ayuda ralentizar la velocidad del reproductor, tal como ocurre en el vídeo de la figura 5, que es una repetición a cámara lenta de los momentos iniciales del vídeo de la figura 4.
Este vídeo auxiliar está ralentizado cinco veces respecto al anterior, lo que significa que la perturbación que vemos viaja 2.000 veces más despacio que la de la cuerda real. Ahora podemos observar con más facilidad que cada una de las dos perturbaciones, cuando no se solapa con la otra, mantiene la amplitud con la que ha sido generada: la que procede de la izquierda es siempre de 1 mm y la que procede de la derecha es siempre de 0,7 mm. Vemos también que la perturbación más amplia, la que procede de la izquierda, circula de izquierda a derecha cuando va por la franja superior y de derecha a izquierda cuando va por la inferior, mientras que la perturbación más pequeña, la que procede de la derecha, circula de derecha a izquierda cuando viaja por la franja inferior y de izquierda a derecha cuando lo hace por la franja superior. Dicho de otra forma, la perturbación mayor sigue siempre el sentido de las agujas del reloj y la menor el sentido contrario al de las agujas del reloj.
Una vez que hemos identificado ambas perturbaciones, podemos observar que cuando se cruzan el desplazamiento que sufre cada punto de la cuerda es la suma de los desplazamientos que hubiera provocado en ella cada una de las perturbaciones por separado, es decir, las dos perturbaciones se superponen linealmente. Como ambas perturbaciones viajan siempre por la misma franja del espacio, las dos por arriba o las dos por abajo, interfieren entre sí de manera constructiva. Y puesto que las dos perturbaciones han comenzado a la vez y se propagan a la misma velocidad, necesariamente se cruzan en la mitad de su camino, en el punto que está a 0,5 m, y es en ese punto donde la perturbación resultante alcanza su desplazamiento máximo. Dado que la amplitud de la perturbación iniciada en el soporte izquierdo es de 1 mm y la provocada por el soporte derecho es de 0,7 mm, la amplitud máxima de la perturbación resultante es de 1,7 mm, que corresponde a un desplazamiento ascendente de la cuerda cuando las perturbaciones se encuentran en la franja superior o a un desplazamiento descendente cuando se encuentran en la franja inferior. Una vez superado su solapamiento cada una de las perturbaciones sigue su camino conservando su individualidad. Hemos podido observar que, como consecuencia de la elasticidad, la perturbación se sigue transmitiendo a través de las fuerzas que ejercen unas bolitas sobre las siguientes, por lo que, cuando cesa la coincidencia de ambas perturbaciones, cada una sigue su camino.
Veamos ahora el vídeo en el que podemos observar cómo se producen las interferencias destructivas:
Este vídeo solo se diferencia del de la figura 4 en que ahora los dos impulsos se dan en sentidos verticales opuestos: mientras que el impulso del soporte izquierdo desplaza la cuerda hacia arriba de su posición de equilibrio, el del soporte derecho la desplaza hacia abajo. Esto hace que las perturbaciones no solo viajen en sentidos opuestos a lo largo de la cuerda, sino que los desplazamientos verticales provocados por las perturbaciones siempre sean opuestos. Podemos observar que ambas perturbaciones se desplazan ahora en el sentido de las agujas del reloj, pero que cuando una se propaga por la franja superior, la otra lo hace por la inferior, y viceversa. Por eso, cuando ambas se cruzan en el punto central de la cuerda, el desplazamiento que sufre ésta es la diferencia de las amplitudes de ambas perturbaciones. Podemos apreciar que cuando la superposición de las dos perturbaciones coincide plenamente, el desplazamiento del punto central de la cuerda es de 0,3 mm (1 – 0,7 = 0,3), hacia arriba o hacia abajo en función de la franja por la que circulen las perturbaciones. También ahora vemos que, una vez que ha concluido el cruce, cada perturbación sigue su camino sin haber sufrido ninguna alteración, hasta reflejarse en el extremo correspondiente.
Formación de ondas estacionarias sobre una cuerda
Una vez que hemos estudiado la propagación, la reflexión y la superposición de las perturbaciones que viajan sobre una cuerda fija, estamos en condiciones de comprender cómo y en qué circunstancias se crean las ondas estacionarias. Y puesto que los sonidos musicales son el resultado de un conjunto armónico de ondas estacionarias, entender cómo se producen estas ondas nos permitirá conocer verdaderamente qué es el sonido musical.
Un movimiento ondulatorio transmite una perturbación de un lugar a otro del espacio, es decir, por naturaleza es viajero. Ahora bien, cuando una onda sinusoidal queda atrapada en algún cuerpo o en alguna región del espacio —como puede ser la cuerda de una guitarra o la columna de aire de una flauta—, las sucesivas interferencias de la onda con su reflejo pueden hacer que su carácter viajero quede disimulado y parezca que la onda se hubiera detenido. En ese momento, el cuerpo o el volumen de aire de la región del espacio en el que la onda ha quedado encerrada comienza a oscilar y la onda viajera se transforma en onda estacionaria.
A continuación vamos examinar, mediante varios vídeos que he fabricado para ello, cómo surgen las ondas estacionarias en la cuerda que nos está sirviendo de modelo. Dado que las ondas estacionarias son el resultado de la superposición de las sucesivas reflexiones de una onda sinusoidal, vamos a introducir en la cuerda oscilaciones sinusoidales, en lugar del impulso gaussiano que hemos utilizado en los vídeos anteriores. Para ello, supondremos que mediante un artilugio mecánico obligamos al soporte que sujeta el extremo izquierdo de la cuerda a realizar un Movimiento Armónico Simple (MAS).
Nuestro objetivo va a ser comprobar que, cuando se introduce una oscilación sinusoidal en una cuerda concreta —definida por su longitud y por la velocidad con la que se propagan en ella las perturbaciones transversales—, sólo se producirán ondas estacionarias si la longitud de la onda creada coincide con el doble de la longitud de la cuerda o si es una parte entera de esta medida. O dicho de otra manera, se generarán ondas estacionarias cuando dentro de la longitud de la cuerda quepan exactamente un número entero de semiondas sinusoidales. En los vídeos de este apartado podremos observar que esto solamente sucede cuando en el tiempo que tarda en completarse una oscilación sinusoidal, la onda recorre exactamente el camino de ida y vuelta a lo largo de la cuerda o una parte entera de este camino. Veremos, así mismo, que las frecuencias de las ondas estacionarias que se pueden producir en una cuerda dada siguen la serie armónica, pues todas ellas son múltiplos de la frecuencia fundamental, que es la frecuencia de la onda estacionaria cuya longitud es el doble de la longitud de la cuerda.
Recordemos que la cuerda ideal sobre la que estamos haciendo la simulación mide un metro de longitud y que la velocidad con la que se propaga por ella cualquier perturbación transversal es de 400 m/s. Por ello, en los vídeos ralentizados 400 veces, la velocidad de la propagación de la onda que observaremos será de 1 m/s, y la duración de 20 segundos corresponderá a las primeras 50 milésimas de segundo de la vibración real. En los vídeos ralentizados 2.000 veces, la velocidad de propagación será de 0,2 m/s y la duración de 30 segundos representará las primeras 15 milésimas de segundo del movimiento real de la cuerda. En todos ellos la amplitud de las oscilaciones sinusoidales introducidas es de 1 mm.
Reflexión de una onda sinusoidal cuya longitud no es una parte entera del doble de la longitud de la cuerda
Pero antes de estudiar las ondas estacionarias vamos a examinar cómo se produce la reflexión de una onda sinusoidal en un extremo fijo de la cuerda cuando la longitud de la onda introducida no es una parte entera del doble de la longitud de la cuerda. Como lo que nos interesa ahora es ver lo que sucede al solaparse la onda incidente con la reflejada, elegiremos una onda cuya longitud sea menor que la longitud de la cuerda. De esta manera, podremos apreciar por separado los momentos en los que se produce el solapamiento de las dos ondas (la incidente y la reflejada) y los momentos en los que solo está presente una de ellas. Por ello, he elegido una onda cuya longitud es de 0,6 metros, la misma que la del impulso gaussiano de los apartados anteriores. El periodo de la oscilación introducida tendrá que ser, por lo tanto, de 1,5 ms. En efecto, dado que la velocidad de propagación de las perturbaciones transversales en nuestra cuerda es de 400 m/s, cuando la oscilación del soporte termine, la onda habrá recorrido 0,6 m (0,0015 x 440 = 0,6). Aunque no sea relevante en este caso, este periodo corresponde, redondeando a décimas de hercio, a una frecuencia de 666,7 Hz.
Así pues, he confeccionado un vídeo en el que se simula el comportamiento de nuestra cuerda ideal cuando introducimos en ella esta única oscilación sinusoidal de 1,5 ms de periodo. Puesto que este vídeo está ralentizado 400 veces, la duración de la oscilación inicial que observaremos en él será de 0,6 segundos.
En el vídeo vemos que una perturbación en forma de onda sinusoidal que ha sido generada por el desplazamiento vertical del soporte izquierdo recorre ininterrumpidamente la longitud de la cuerda, reflejándose de forma invertida cada vez que alcanza uno de los extremos fijos. A diferencia de los vídeos anteriores, ahora nos sorprende el carácter artificial del movimiento que realiza la cuerda. Ello se debe a la introducción repentina de una única oscilación sinusoidal y a su cese instantáneo, sin transición alguna, ni al comienzo ni al final. Aunque he procurado dotar de la mayor verosimilitud posible al movimiento de la cuerda, no podemos olvidar que estamos ante una simulación de carácter didáctico, en la que es necesario aislar el fenómeno que nos interesa estudiar, aun a consta de una apariencia artificiosa.
Distinguimos en el vídeo dos situaciones claramente diferenciadas: los momentos en los que la onda va y viene por el medio de la cuerda y los momentos en los que esa onda se deforma, dando lugar a una fugaz semionda, cuando se refleja en los soportes de los extremos. Respecto a los primeros, no hay nada que no hayamos visto antes. Observamos cómo la oscilación provocada por el Movimiento Armónico Simple que ha realizado el soporte, se dibuja en la cuerda en forma de onda sinusoidal. Si pensamos en los tiempos en los que suceden los acontecimientos en el vídeo, podemos verificar también que la longitud de la onda introducida es de 0,6 metros. Puesto que la velocidad con la que se propagan las perturbaciones en la cuerda del vídeo es de 1 m/s, en los 0,6 segundos que ha tardado la oscilación en completarse, la onda introducida habrá recorrido 0,6 m. En efecto, si detenemos el vídeo en cualquier instante en el que la onda se encuentre en una posición intermedia, podremos comprobar que su longitud es de 0,6 metros.
Como lo que nos interesa ahora en particular es estudiar lo que sucede en los momentos en los que se produce la reflexión de la onda en cada uno de los soportes fijos en los que termina la cuerda, he fabricado un vídeo auxiliar con el movimiento de la cuerda ralentizado 5 veces más que en el vídeo anterior. En él se representan también las dos cuerdas imaginarias que hemos visto en el vídeo de la figura 3, pues nos sirven para interpretar la reflexión como la superposición de dos ondas virtuales, la incidente y la reflejada, que viajarían por ellas.
Igual que en el vídeo anterior, vemos que sobre la cuerda real —representada por las bolitas unidas por muellecillos— se desplaza una onda sinusoidal que se refleja cada vez que alcanza uno de los extremos fijos. Vemos también dos cuerdas virtuales que no están sujetas a ningún soporte y que, como en el vídeo de la figura 3, debemos imaginar prolongándose por ambos lados a través de un espacio imaginario que no está representado en este vídeo. Por la cuerda amarilla viaja, de izquierda a derecha, la perturbación original en los primeros segundos del vídeo, y luego los sucesivos reflejos que se producen en el soporte izquierdo (esto es, las ondas sinusoidales provenientes del otro lado del hipotético espejo situado a la izquierda de la cuerda). Por la cuerda turquesa viajan, de derecha a izquierda, las ondulaciones reflejadas en el soporte derecho (es decir, las ondas que llegan desde el espacio imaginario de la derecha), las cuales son del mismo periodo, amplitud y longitud de onda que las de la cuerda amarilla, pero invertidas. Ya he explicado, a propósito del vídeo de la figura 3, la razón por la que la suma de los desplazamientos de las cuerdas auxiliares en los puntos extremos fijos es siempre cero.
Ahora vamos a prestar atención a lo que sucede cuando se produce la superposición entre la onda incidente y la reflejada en los extremos fijos de la cuerda. Si nos fijamos en el soporte de la derecha, vemos que en el momento en el que la onda que viaja por la cuerda amarilla comienza a atravesar el soporte, también lo hace la onda turquesa que, invertida, proviene del otro lado del supuesto espejo. Como una onda es la inversa de la otra y ambas viajan a la misma velocidad en sentidos opuestos, en el momento en el que ambas están a la mitad del cruce, las dos, que en ese momento tienen la forma de una semionda sinusoidal inferior, coinciden exactamente. Lo mismo sucede en el soporte derecho, con la única diferencia de que, en ese caso, las semiondas que coinciden son las superiores. En ambos momentos, vemos que la cuerda adquiere su desplazamiento máximo, hacia abajo o hacia arriba, respectivamente.
Veamos una instantánea de este último vídeo que representa un momento inmediatamente anterior a producirse la coincidencia exacta de las dos ondas virtuales cuando se cruzan en el soporte derecho (si fuera en el momento exacto no podríamos distinguir las dos cuerdas virtuales, pues coincidirían exactamente).
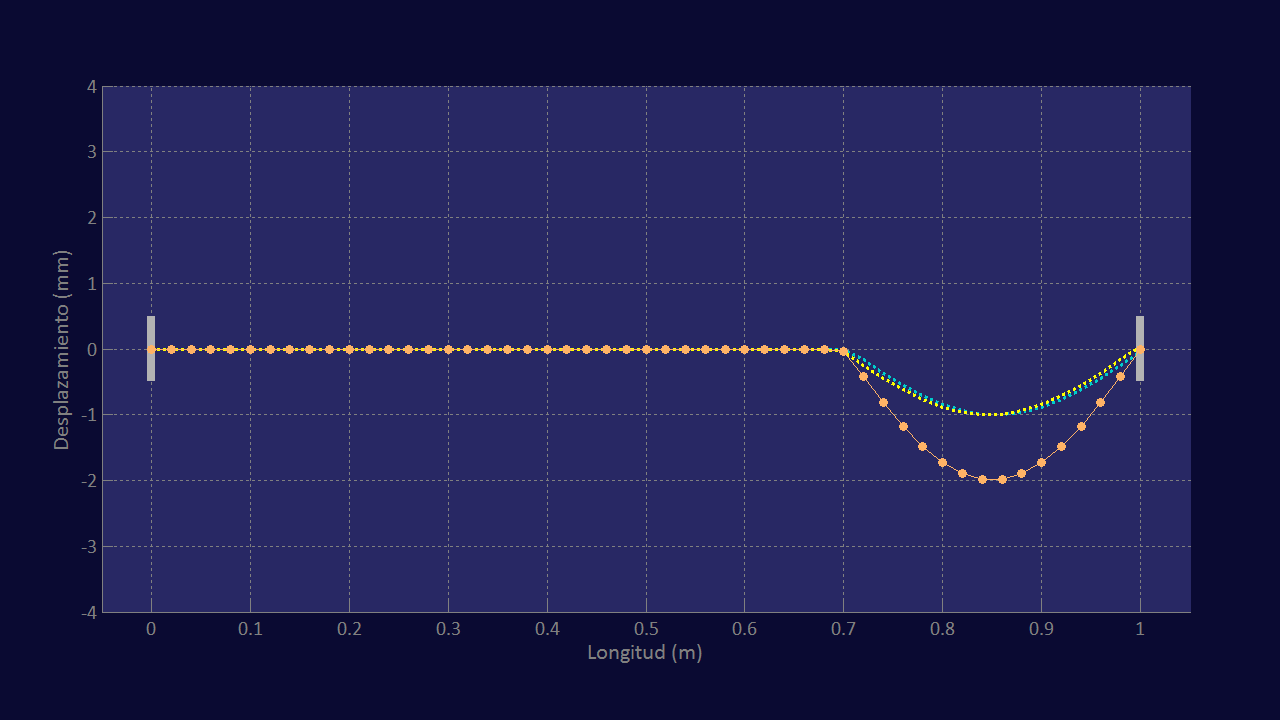
En la figura podemos observar que en el momento de la coincidencia, tanto la onda incidente como la reflejada tienen la forma de una semionda sinusoidal inferior. Teniendo en cuenta que la suma de dos ondas sinusoidales de la misma fase es también una onda sinusoidal de la misma fase cuya amplitud es la suma de las amplitudes de las dos ondas componentes, la cuerda real adquiere también la forma de una semionda sinusoidal de la misma fase, cuya amplitud es el doble de la de las ondas virtuales. En la gráfica vemos que la semionda formada en la cuerda real, la de las bolitas, tiene una amplitud de 2 mm, el doble de la que tiene la onda cuando no está solapada.
Resumiendo, mediante los vídeos de las figuras 7 y 8 hemos podido observar que las semiondas creadas en la cuerda real en cada reflexión duran solamente un instante, pues a continuación esa semionda fugaz se diluye y se dibuja de nuevo en la cuerda la forma de la onda completa. Así pues, la onda sigue siendo viajera, pues en esta cuerda la oscilación introducida no ha generado una onda estacionaria.
Generación de una onda estacionaria en el modo fundamental de vibración
A continuación examinaremos lo que sucede al introducir en la cuerda, mediante el desplazamiento vertical del soporte izquierdo, una oscilación de un periodo tal que sea capaz de generar en ella una onda sinusoidal de longitud doble de lo que mide la cuerda. Veremos que cuando la onda termine de realizar por primera vez su recorrido de ida y vuelta a lo largo de la cuerda, su carácter viajero quedará enmascarado y la cuerda entera comenzará a oscilar de forma unitaria, realizando un Movimiento Armónico Simple de la misma frecuencia que la de la oscilación inicial que la ha generado. Cuando esto ocurre decimos que se ha producido una onda estacionaria en el modo fundamental de vibración o primer modo.
Para generar una onda estacionaria de estas características en la cuerda que nos sirve de modelo (que, recordemos, mide 1 metro y tiene una velocidad de propagación de 400 m/s), la longitud de la onda sinusoidal que viaje por ella deberá tener 2 metros y, por lo tanto, el periodo de la oscilación inicial que deberemos introducir tendrá que ser de 5 milésimas de segundo. En efecto, en 5 ms la onda habrá recorrido los 2 metros que mide el camino de ida y vuelta a lo largo de la cuerda (440 x 0,005 = 2). La frecuencia de la oscilación será, pues, de 200 Hz (1/0,005 = 200).
Como en los casos anteriores, he fabricado un vídeo que reproduce, ralentizado 400 veces, el movimiento de la cuerda en estas condiciones. El periodo de la oscilación inicial que observaremos en el vídeo será, por lo tanto, de 2 segundos y su frecuencia de 0,5 Hz. La velocidad de propagación que veremos será de 1 m/s.
Al igual que en el vídeo de la figura 7, como consecuencia de la superposición de la onda con su reflejo, se crea en la cuerda una semionda sinusoidal inferior. La diferencia reside en que ahora la semionda abarca la cuerda entera y en que la cuerda conserva la forma de semionda durante toda la duración del vídeo, alternándose entre semionda inferior y semionda superior. Aparentemente ya no se transmite ninguna perturbación por la cuerda; en su lugar, oscila la cuerda en su conjunto como un todo, repitiendo toda ella el movimiento oscilatorio que ha sido introducido por el soporte. La onda ha dejado de viajar a lo largo de la cuerda y se ha transformado en una onda estacionaria. La frecuencia con la que oscila la cuerda es la misma que la de la oscilación que la ha generado, en nuestro vídeo, que está ralentizado 400 veces, es decir, 0,5 Hz. En efecto, podemos observar que cada 2 segundos la cuerda realiza una oscilación completa.
Vemos también que, una vez formada la onda estacionaria, cada punto de la cuerda oscila de forma sinusoidal, en fase con todos los demás, con una amplitud que es siempre la misma para cada punto y que depende únicamente de su posición en la cuerda. Observamos que los puntos extremos permanecen fijos y que el punto situado en la mitad de la cuerda es el que alcanza la mayor amplitud.
La pregunta que tenemos que responder ahora es: ¿Por qué se ha producido esto? Para entender con más detalle lo que ocurre vamos a ver un vídeo que describe, cinco veces más despacio que el vídeo anterior, los momentos iniciales en los que se crea la onda estacionaria. En él aparecen las cuerdas virtuales que hemos visto antes y que nos van a ayudar a entender cómo las constantes interferencias entre las ondas reflejadas en ambos extremos fijos dan lugar a la onda estacionaria.
Con ayuda de las cuerdas virtuales auxiliares, en el vídeo podemos ver que lo que está sucediendo por debajo de esa apariencia de estabilidad es que los sucesivos reflejos de la onda viajera están interfiriendo entre sí, dando lugar a la formación de esa onda que parece haberse detenido. En el vídeo vemos que, como consecuencia de los sucesivos reflejos, la onda sinusoidal amarilla viaja ininterrumpidamente de izquierda a derecha, y la turquesa de derecha a izquierda.
En los momentos iniciales del vídeo, podemos apreciar que cuando la onda incidente, la de color amarillo, alcanza el soporte derecho, comienza a surgir invertida la onda reflejada, la de color turquesa. Como he explicado a propósito del vídeo de la figura 8, cuando ambas ondas imaginarias completan la mitad de su recorrido, coinciden plenamente y la cuerda real, la de las bolitas, adquiere la forma de una semionda sinusoidal inferior. Dado que, en este caso, la longitud de la onda es de 2 metros, la semionda abarca la longitud entera de la cuerda y, por lo tanto, se termina de formar en el instante exacto en el que el soporte izquierdo ha completado su oscilación. Esta coincidencia —que se produce como consecuencia de que el periodo de la oscilación introducida y la velocidad de propagación de la cuerda dan lugar a una onda de longitud doble que la de la cuerda— es la causa de que la cuerda comience a oscilar de forma unitaria y se cree una onda estacionaria en el primer modo de vibración. Veamos en la figura de abajo el momento inmediatamente anterior a la formación de esta semionda sinusoidal.
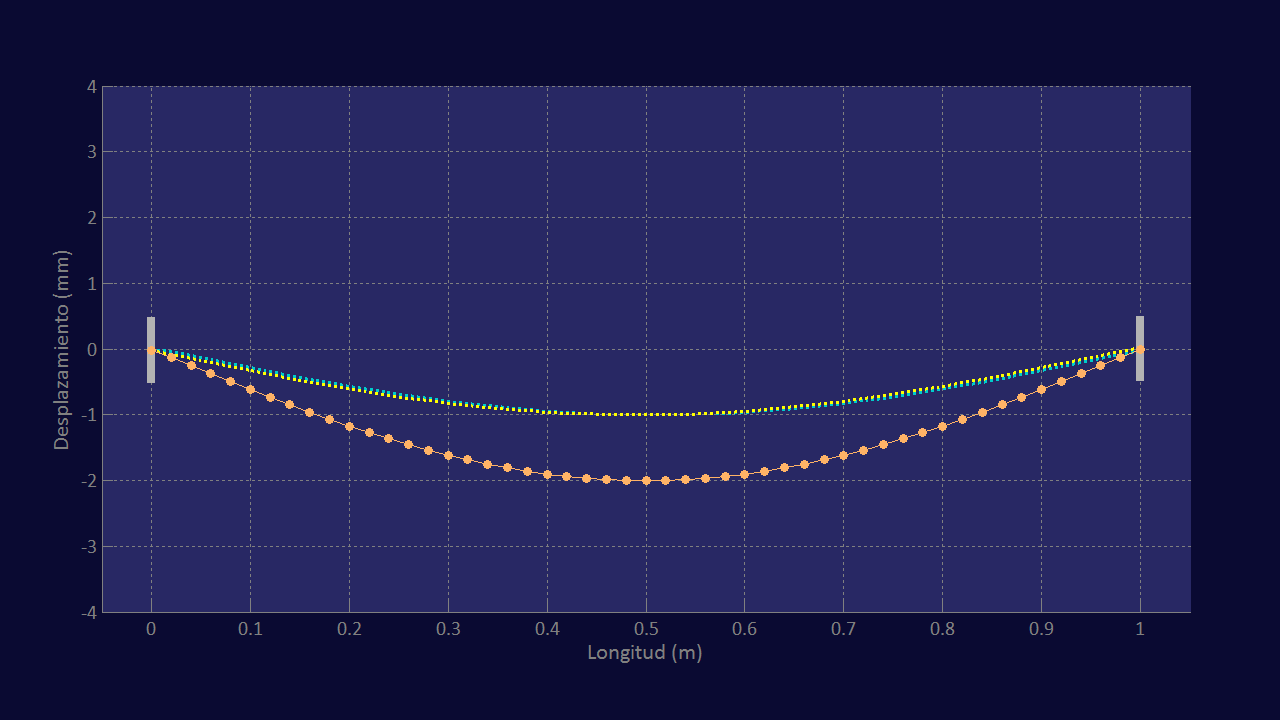
Vemos que la cuerda entera está a punto de adquirir la forma de una semionda sinusoidal y que, al coincidir las dos ondas virtuales, su amplitud alcanza el valor máximo, 2 mm.
Tenemos que entender ahora por qué esta forma que adquiere la cuerda no se diluye, como en el caso del vídeo de la figura 8, sino que la ondulación de la cuerda va modificando su amplitud y alternando su forma entre una semionda inferior y una semionda superior.
Para ello, tenemos que tener presente que la suma de dos ondas sinusoidales de la misma longitud de onda es otra onda sinusoidal de esa misma longitud, cuya amplitud depende de la diferencia de fase entre las dos ondas componentes. Al viajar las dos ondas en dirección opuesta, el desplazamiento hacia la derecha de la onda que va por la cuerda amarilla es compensado por el desplazamiento hacia la izquierda de la onda turquesa, por lo que la cuerda real, la de las bolitas, siempre conserva la misma fase, manteniendo, por lo tanto, la forma de una semionda sinusoidal. Puesto que las dos ondas auxiliares viajan a la misma velocidad en direcciones opuestas, siempre se cruzan en el medio, pasando de coincidir plenamente, cuando ambas cuerdas virtuales forman una semionda inferior o superior, a oponerse por completo, dando lugar a que la cuerda adquiera, en el instante en el que pasa por la posición de equilibrio, la forma rectilínea.
Dicho de otra manera, las cuerdas auxiliares pasan continuamente de estar en fase a estar en oposición de fase. Pero siempre los adelantos de una se compensan con los retrasos de la otra, por lo que la resultante, la de la cuerda real, es siempre una semionda inferior o una semionda superior, según sea la zona en la que coincidan las ondas virtuales. Los desfases entre las ondas virtuales se traducen en diferencias de amplitud de la onda resultante: cuando ambas están en fase —es decir, cuando coinciden— la amplitud es máxima, como hemos visto en la figura 12; conforme se desfasan, yendo una hacia la derecha y la otra hacia la izquierda, la amplitud de la cuerda real disminuye; y cuando llegan a estar en oposición de fase, la amplitud se anula y en ese instante la cuerda recobra su forma rectilínea, como se puede ver en la figura de abajo.

Por otra parte, dado que el desplazamiento de cualquier punto de la cuerda real es la suma de los desplazamientos de los puntos correspondientes de la onda incidente y la reflejada, en toda onda estacionaria hay puntos cuyo desplazamiento es siempre nulo y otros cuyo desplazamiento alcanza el valor máximo. Los puntos que son fijos se denominan nodos, y en este modo fundamental de vibración son sólo los puntos extremos de la cuerda. Los puntos que oscilan con una amplitud máxima se denominan vientres o antinodos, y en este modo, sólo lo es el punto medio, aquél en el que siempre se cruzan las dos ondas virtuales. La amplitud con la que oscila este punto es el doble de la amplitud de la oscilación introducida, en este caso podemos ver que es de 2 mm.
Así pues, el modo primero de vibración se caracteriza porque la cuerda entera oscila de forma unitaria. En consecuencia, tiene un solo vientre en el punto central de la cuerda y dos nodos que están situados en los puntos extremos. La frecuencia de este primer modo de vibración es la que corresponde a una longitud de onda doble de la longitud de la cuerda. En nuestra cuerda ideal, sobre la que estamos realizando la simulación, la frecuencia de este primer modo de vibración es de 200 Hz.
Generación de ondas estacionarias en los modos de vibración armónicos
Ahora vamos a comprobar que también se producen ondas estacionarias en nuestra cuerda cuando la oscilación que introducimos al desplazar el soporte izquierdo da lugar a una onda cuya longitud es una parte entera del doble de la longitud de la cuerda. O, dicho de otra manera, cuando introducimos oscilaciones sinusoidales cuyo periodo es tal que, al reflejarse la perturbación en los extremos fijos de la cuerda, se crean un número entero de semiondas. Para que este requisito se cumpla, el periodo de las oscilaciones iniciales tendrá que ser la mitad, la tercera parte, la cuarta parte o cualquier parte entera del periodo que ha producido la onda estacionaria en el modo de vibración fundamental. Por ello, la frecuencia de estas oscilaciones iniciales —que será la misma con la que oscilará la cuerda cuando se formen en ella las ondas estacionarias— tendrá que ser el doble, el triple, el cuádruple o cualquier otro múltiplo entero de la frecuencia fundamental de vibración. Ello explica que estos modos naturales de vibración se denominen armónicos.
Vamos a detenernos a continuación en observar cómo se produce el segundo modo de vibración y luego generalizaremos los conceptos aprendidos al resto de los modos armónicos.
Para lograr que nuestra cuerda ideal se ponga a vibrar en el segundo modo de vibración, la longitud de la onda que deberemos generar tendrá que ser de 1 metro. Por ello, el periodo con el que deberá oscilar el soporte izquierdo para introducir la perturbación tendrá que ser de 2,5 ms. En efecto, dado que la velocidad de la cuerda es de 400 m/s, en 2,5 ms la onda habrá recorrido 1 metro (400 x 0,0025 = 1). La frecuencia de la oscilación inicial será, por lo tanto, de 400 Hz. Tenemos que tener en cuenta también que, para que se produzca el solapamiento de la onda incidente con la reflejada en el segundo modo de vibración, deberemos introducir en la cuerda dos oscilaciones completas.
He fabricado un vídeo que simula el comportamiento de nuestra cuerda ideal cuando se introducen en ella dos oscilaciones sinusoidales de ese periodo de 2,5 ms. También ahora el movimiento de la cuerda está ralentizado 400 veces, con lo cual el periodo de la oscilación que observaremos será de 1 segundo y su frecuencia, por lo tanto, de 1 Hz.
En el vídeo podemos observar que en el mismo instante en el que el soporte izquierdo ha terminado de realizar las dos oscilaciones y se ha quedado fijo, en la cuerda se han formado dos semiondas, una inferior y otra superior, es decir, se ha creado una onda sinusoidal entera. De modo similar a lo que hemos visto en el caso de la onda estacionaria en el modo fundamental de vibración, a partir de ese momento desaparece el carácter viajero de la onda y la cuerda comienza a oscilar. La diferencia reside en que ahora oscila como si estuviera dividida en dos partes. La forma que adquiere la cuerda en su oscilación es la de una onda completa.
Ahora hay un nuevo punto fijo, un nodo, que está en el medio de la cuerda (con lo que en total hay tres nodos), y dos puntos de desplazamiento máximo, dos antinodos o vientres, que están en la mitad de cada semionda, uno a 0,25 m y el otro a 0,75 m.
La frecuencia con la que vemos oscilar la cuerda en este vídeo es el doble de la que tenía en el anterior: ahora es de 1 Hz, que corresponde, en la cuerda de la realidad, a 400 Hz. Esta frecuencia es la misma que la de las oscilaciones iniciales que han generado la onda estacionaria.
Dado que en el modo segundo de vibración la cuerda adquiere la forma de una onda sinusoidal completa, podremos apreciar más claramente cómo surge una onda estacionaria. Para verlo con más detalle he fabricado un vídeo con los momentos iniciales del movimiento de la cuerda, ralentizados 5 veces respecto al vídeo anterior o, lo que es lo mismo, 2.000 veces respecto al movimiento de la cuerda real. Este vídeo corresponde a las primeras 15 milésimas de segundo del movimiento de la cuerda real. También ahora la cuerda real, representada por las bolitas, va acompañada de las cuerdas virtuales auxiliares, la amarilla y la azul turquesa.
Puesto que ahora la longitud de la onda es la misma que la de la cuerda, podemos observar que justamente cuando la perturbación inicial —que viaja de izquierda a derecha por la cuerda auxiliar amarilla— alcanza el soporte derecho, se termina de formar en la cuerda una onda sinusoidal completa. Luego, justo cuando empieza a surgir en la cuerda la segunda ondulación sinusoidal desde el soporte izquierdo, esa primera perturbación se refleja en el soporte derecho y regresa invertida, de derecha a izquierda, por la cuerda virtual turquesa. Podemos ver después que, en el instante en el que la primera onda ha terminado de recorrer el camino de ida y vuelta a lo largo de la cuerda y ha alcanzado de nuevo el soporte izquierdo, la segunda onda ha llegado al soporte derecho. En ese mismo instante, la onda incidente y la reflejada coinciden plenamente y la cuerda real dibuja la forma entera de una onda o, lo que es lo mismo, la de dos semiondas opuestas consecutivas. En la figura de abajo se muestra el instante previo a esta coincidencia.
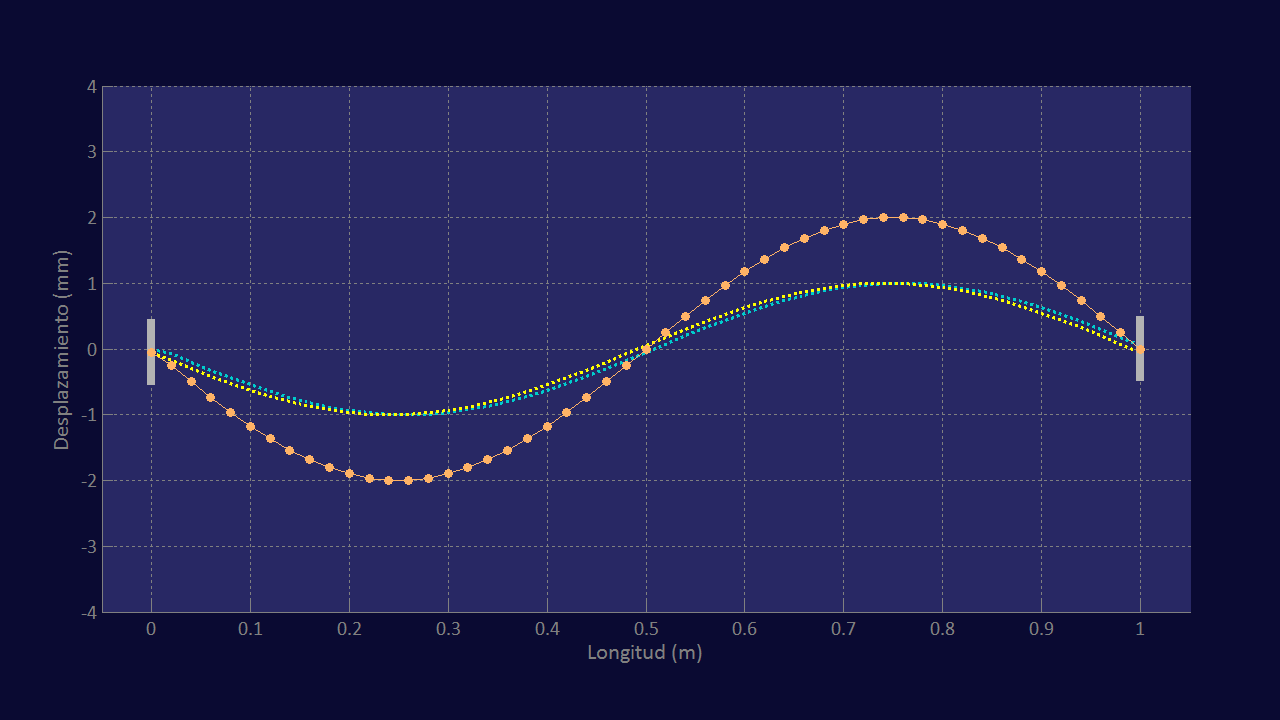
En la figura podemos apreciar que en ese instante las cuerdas virtuales prácticamente coinciden, con lo que, al sumarse los desplazamientos de ambas, el desplazamiento vertical de cada uno de los puntos de la cuerda real alcanza su valor máximo, dando como resultado una onda sinusoidal cuya amplitud es el doble de la amplitud de la oscilación introducida, es decir, 2 mm.
Si volvemos al vídeo de la figura 15, podemos fijarnos en que, a partir del momento en el que la cuerda adquiere la forma de una onda completa, el desplazamiento hacia la derecha de la onda virtual incidente —la que viaja por la cuerda amarilla— es compensado por el desplazamiento hacia la izquierda de la onda virtual reflejada —la que viaja por la cuerda turquesa—, de modo que desde ese momento la cuerda, que parece estar dividida en dos partes, oscila de forma estable, como si ya no se propagara ninguna perturbación por ella.
Atendamos ahora a lo que ocurre cuando la cuerda oscila. Nos damos cuenta de que pasa por dos situaciones extremas. Una es el momento en el que las cuerdas auxiliares coinciden completamente, con lo que la ondulación de la cuerda real alcanza su máxima amplitud, como hemos visto en la figura 16; otra es el momento en el que las cuerdas virtuales están en oposición de fase, con lo que los desplazamientos de todos los puntos de la cuerda se anulan y ésta pasa por su posición de equilibrio, como podemos ver en la figura de abajo.

En el vídeo de la figura 15 podemos apreciar que, como consecuencia también de que ambas ondas virtuales se desplazan a la misma velocidad en sentidos opuestos, se cruzan siempre en los mismos puntos y se oponen siempre en los mismos puntos. Dado que el desplazamiento de cualquier punto de la cuerda real es la suma de los desplazamientos de los puntos correspondientes de las cuerdas virtuales, los puntos en los que éstas se cruzan oscilan con la máxima amplitud y son los vientres o antinodos de la onda estacionaria, mientras que los puntos en los que siempre se oponen permanecen fijos y constituyen los nodos. En la figura 17 podemos ver que las ondas virtuales se cruzan en 0,25 m y 0,75 m, que corresponden a los vientres de la onda real que hemos visto en el vídeo, y se oponen en 0 m, 0,5 m y 1 m, que corresponden a los nodos de la onda real.
Podemos generalizar las ideas que hemos visto respecto al primero y segundo modo de vibración a cualquier caso en el que la frecuencia de las oscilaciones iniciales sea múltiplo de la frecuencia del modo fundamental. En cualquiera de esos modos de resonancia armónicos, la longitud de la onda generada por la oscilación inicial será necesariamente una parte entera del doble de la longitud de la cuerda (que, recordemos, coincide con la longitud de la onda en el modo de resonancia fundamental), de forma que la cuerda entera oscilará dividida en tantas partes como semiondas se puedan formar en ella.
En el vídeo de abajo se simula la generación de una onda estacionaria en el tercer modo de vibración. El periodo de las oscilaciones introducidas tendrá que ser, en este caso, la tercera parte del periodo necesario para producir la onda estacionaria en el modo fundamental, es decir, 5/3 ms. Por ello, la frecuencia correspondiente será el triple de la frecuencia fundamental, esto es, 600 Hz, si bien, al estar el vídeo ralentizado 400 veces, la frecuencia que observaremos en él será de 1,5 Hz. La longitud de la onda será también la tercera parte del doble de la longitud de la cuerda, esto es, 2/3 m, es decir, redondeando a milímetros, 0,667 m. Para que se solapen completamente la onda introducida con su reflejo necesitaremos ahora tres oscilaciones iniciales.
Podemos observar que, al terminar de completarse las tres oscilaciones iniciales del soporte, la cuerda comienza a vibrar sin que parezca que se propague ya ninguna perturbación por ella. En este caso la cuerda adquiere la forma de tres semiondas sinusoidales, consecutivas y opuestas, que oscilan al ritmo de la frecuencia introducida. Vemos que en este modo estacionario de vibración se forman 4 nodos —en los puntos 0, 0,3333, 0,6666 y 1—, que dividen la cuerda en tres partes, y tres vientres entre los nodos. Puesto que la frecuencia que resulta es el triple de la del modo primero de vibración, cuando es excitado este modo, producirá el tercer armónico.
Algo parecido podríamos hacer para generar el cuarto modo de vibración, con la diferencia de que deberíamos introducir cuatro oscilaciones. En ese caso el periodo de la oscilación introducida deberá ser la cuarta parte del periodo fundamental y su frecuencia, cuádruple, es decir, deberá tener un periodo de 1,25 ms y, por lo tanto, una frecuencia de 800 Hz. Ello dará lugar a una longitud de onda de 0,5 m. Veámoslo en un nuevo vídeo.
La frecuencia representada en el vídeo es de 2 Hz, pues el movimiento de la cuerda está ralentizado 400 veces respecto a la vibración real que está simulando. Podemos observar que en las ondas estacionarias que se forman en el cuarto modo de vibración hay 5 nodos —en los puntos 0, 0,25, 0,5, 0,75 y 1—, que dividen la cuerda en cuatro semiondas, y cuatro vientres entre los nodos. Así pues, la frecuencia de 800 Hz, que es cuatro veces la del modo primero de vibración de esta cuerda, corresponde al cuarto armónico.
Y algo similar podríamos observar en los restantes modos de vibración. Su número, en principio, sería infinito. En la realidad, sin embargo, la pérdida de elasticidad de la cuerda para longitudes de onda pequeñas hace que el número de modos armónicos de vibración sea limitado.
De los vídeos que hemos visto en este apartado dedicado a la formación de ondas estacionarias podemos sacar la conclusión de que la cuerda fija en sus extremos tiene la propiedad de crear ondas estacionarias a frecuencias que son múltiplos enteros de una frecuencia fundamental determinada, es decir, en modos de vibración armónicos. La frecuencia fundamental depende tanto de la velocidad de propagación de la perturbación a lo largo de esa cuerda, como de la longitud de ésta. El periodo de la oscilación que da lugar a la frecuencia fundamental coincide con el tiempo que tarda la perturbación en realizar el camino de ida y vuelta a lo largo de la cuerda. Y también se crean ondas estacionarias cuando se introducen 2, 3, 4 o cualquier número entero de oscilaciones en ese tiempo que tarda la perturbación en ir y volver. Eso quiere decir que la cuerda tiene unos modos naturales de vibración, los cuales son también llamados modos de resonancia. A continuación veremos por qué se llaman así y lo que sucede cuando son excitados.
La resonancia
Cualquier músico ha sufrido alguna vez la desagradable experiencia de que algún objeto de su entorno empezaba a emitir un sonido cuando daba una determinada nota con su instrumento, sin que le resultara nada sencillo determinar su procedencia. Al cabo, se ha encontrado con un cenicero metálico, una lámpara de cristal o un objeto cualquiera que estaba vibrando. Ocurría simplemente que el objeto en cuestión resonaba con la nota musical que estaba emitiendo el instrumento: la vibración producida por esa nota tenía un componente frecuencial que coincidía con alguna de las frecuencias naturales de vibración del objeto, de modo que éste se ponía a resonar.
La resonancia se produce porque un cuerpo que vibra excita a otro que es capaz de vibrar. Un cuerpo entra en resonancia cuando alguna de las frecuencias del sistema excitador coincide con alguna de las frecuencias naturales de vibración que ese cuerpo posee, de modo que la perturbación no se limita a pasar a través de él, sino que se retroalimenta positivamente, dando lugar a una onda estacionaria cuya amplitud se va incrementando con el paso del tiempo. La resonancia despierta los modos de vibración que por naturaleza posee cada objeto y por eso a estos modos normales o naturales de vibración se les llama también modos de resonancia.
Un ejemplo tomado de la vida cotidiana que nos puede servir para comprender el fenómeno de la resonancia es el de un columpio. Pensemos que tenemos a un niño columpiándose y queremos que cada vez gane más altura y que el columpio se balancee más y más. El columpio, al igual que cualquier péndulo, tiene una frecuencia natural de oscilación, la cual depende de su longitud. Si empujamos el columpio de forma periódica, haciendo que nuestros impulsos se produzcan siempre en el mismo estado de la oscilación, el columpio irá ganando en altura; si, por el contrario, impulsamos el columpio cuando se nos ocurra, con total independencia del estado de oscilación, no incrementaremos la amplitud de sus oscilaciones, sino que probablemente lo frenaremos. En definitiva, si impulsamos el columpio siempre con la misma frecuencia y ésta coincide con la frecuencia natural de oscilación de ese columpio concreto (por ejemplo, si lo impulsamos siempre cuando pasa lo más próximo al suelo), el columpio irá acumulando esa energía y progresivamente la amplitud de sus oscilaciones aumentará.
Examinemos ahora cómo se produce la resonancia en la cuerda que estamos utilizando para nuestras simulaciones. Recordemos que mide 1 m de longitud, que está fija en sus extremos y que tiene, por razón de su masa y de la tensión a la que está sometida, una velocidad de propagación de las perturbaciones transversales de 400 m/s. Como consecuencia de ello, tal como hemos visto en el apartado anterior, en nuestra cuerda se puedan crear ondas estacionarias en frecuencias que sean múltiplos enteros de 200 Hz. Y esto quiere decir que cuando la cuerda entre en contacto con una vibración en alguna de estas frecuencias, se pondrá en resonancia con ella y empezará a vibrar por simpatía: con una frecuencia de 200 Hz dará el primer modo de resonancia o fundamental; con una de 400 Hz, el segundo modo de resonancia; con 600 Hz, el tercero, y así sucesivamente. Así pues, si en nuestra simulación hacemos que la frecuencia con la que oscila el soporte que introduce la perturbación coincida con una de esas frecuencias naturales de vibración, la cuerda se pondrá a vibrar en resonancia.
A diferencia de los casos anteriores, ahora vamos a introducir en la cuerda oscilaciones de modo continuo, unas oscilaciones de amplitud muy pequeña, de 0,1 mm, pero que se mantienen durante cierto periodo de tiempo, exactamente durante 50 ms. Lo que nos interesa es comprobar cómo la amplitud de la oscilación que se genera en la cuerda va creciendo rápidamente a medida que pasa el tiempo.
Empezaremos viendo lo que ocurre cuando el soporte oscila durante 50 ms a una frecuencia de 200 Hz, es decir, la frecuencia del modo fundamental o primero de resonancia de nuestra cuerda. En el vídeo de abajo, que está ralentizado 400 veces, la frecuencia será de 0,5 Hz, con lo que podremos observar una oscilación completa cada 2 segundos.
Vemos que enseguida se crea una onda estacionaria en el primer modo de resonancia, por lo que la cuerda entera oscila de manera unitaria. Pero vemos también, y esto es lo más importante, que la amplitud de la oscilación crece de manera muy rápida, de tal forma que cuando el soporte se detiene al concluir los primeros 50 ms de la realidad (o los primeros 20 segundos del vídeo), la amplitud de la oscilación de la cuerda ha alcanzado ya 2 mm. Es decir, han bastado 50 ms de oscilación del soporte para multiplicar la amplitud de esa oscilación inicial por 20 veces. Sucede que el movimiento del soporte se acopla con las sucesivas reflexiones de la cuerda, de tal modo que la energía se acumula y eso hace crecer la oscilación de la cuerda, de modo semejante a lo que ocurre en el columpio.
Ahora examinaremos lo que sucede cuando el soporte oscila con otra de las frecuencias de resonancia naturales de nuestra cuerda, en este caso 400 Hz, que corresponde al segundo modo de resonancia. En el vídeo, ralentizado 400 veces, la frecuencia será de 1 Hz.
Vemos que en este caso se crea también una onda estacionaria, ahora en el modo segundo. En efecto, la cuerda oscila dividida por la mitad en dos partes. Cuando el soporte deja de moverse el punto medio permanece ya estable y se crea en él un nodo. También ahora podemos apreciar que la mínima amplitud con la que oscila el soporte es capaz de provocar una gran respuesta en la oscilación de la cuerda. Comprobamos, pues, que la cuerda resuena también a la frecuencia de 400 Hz.
Para experimentar que la resonancia se produce solo cuando la oscilación que introducimos tiene una frecuencia que coincide con alguno de los modos de resonancia naturales de nuestra cuerda, vamos a ver lo que sucede cuando forzamos a la cuerda a vibrar a una frecuencia alejada de cualquiera de esos modos. En concreto, vamos a forzar a la cuerda mediante una oscilación constante del soporte izquierdo a 285 Hz de frecuencia. En el vídeo, al estar ralentizado 400 veces, la frecuencia del soporte será aproximadamente de 0,7 Hz.
La duración del vídeo es de 33 segundos, que corresponden aproximadamente a 82 milésimas de segundo del movimiento real de la cuerda. A pesar de que durante todo este tiempo el soporte izquierdo se mantiene oscilando, vemos que no es capaz de generar en la cuerda una onda estacionaria. El soporte fuerza a vibrar a la cuerda a la misma frecuencia con la que oscila, 285 Hz en la realidad y 0,7 Hz en el vídeo, pero, como esta frecuencia no corresponde a ninguna de las frecuencias naturales de resonancia de la cuerda, la oscilación del soporte no se acopla con la onda que se transmite a lo largo de la cuerda y no genera ninguna onda estacionaria. Además, la amplitud con la que oscila la cuerda forzada por el soporte es, por ello mismo, muy pequeña.
En resumen, cuando un cuerpo vibra siempre lo hace a la misma frecuencia que posee aquello que lo fuerza a vibrar. La diferencia es que si esa frecuencia coincide con alguna que posee el cuerpo receptor por su propia naturaleza, esa fuerza se transmite muy eficazmente, acoplándose y amplificándose, mientras que si no se produce esa coincidencia, la eficacia es mucho menor.
La resonancia se produce siempre en un contexto de oscilaciones forzadas. La resonancia implica dos partes. Por un lado, la parte activa: un cuerpo o sistema que vibra y que con sus vibraciones excita o impulsa a otro. Por otro, la parte pasiva: un cuerpo o sistema que, por su propia constitución, posee una o varias frecuencias naturales de vibración. Al poner en relación estas dos partes, siempre el resultado será que la frecuencia de la vibración del cuerpo o sistema pasivo será la misma que la del sistema impulsor o activo, con independencia de cuál fuera su frecuencia natural de vibración. Ahora bien, cuando la frecuencia del sistema impulsor se aproxima mucho a una de las frecuencias naturales del sistema pasivo, la facilidad con la que la energía del sistema impulsor se transmite al sistema pasivo hace que la amplitud de las vibraciones de este sistema pasivo crezca de forma extraordinaria.
Como conclusión podemos decir, que, en líneas generales, cuando coincide la frecuencia de la fuerza excitante y la frecuencia natural del sistema pasivo, se produce un cambio cualitativo importante. La resonancia nos muestra como una fuerza en sí misma pequeña puede crear un efecto grande. Este efecto será más evidente conforme las fuerzas de fricción o cualquier otra que se oponga al movimiento sean menores. En el caso de nuestra cuerda ideal en la que hemos descartado cualquier fuerza de amortiguación este crecimiento es máximo.
Generación del sonido armónico
Una vez que hemos visto que la cuerda, por sus propias características físicas, posee unos modos naturales de vibración que son armónicos y que estos modos resuenan cuando coinciden con alguna o algunas de las frecuencias que están presentes en la perturbación que la excita, estamos en condiciones de entender en qué consiste y cómo se produce la vibración armónica.
Habitualmente una cuerda, como cualquier otro cuerpo capaz de vibrar, vibra simultáneamente en varios modos de resonancia. Esto da lugar a que el movimiento de la cuerda evolucione de una forma aparentemente compleja.
Vamos a comenzar observando un caso sencillo: el movimiento a cámara lenta que realiza la cuerda de nuestra simulación cuando vibra simultáneamente en los dos primeros modos de resonancia. Para ello, he fabricado un vídeo en el que el movimiento del soporte que provoca la vibración de la cuerda es una oscilación armónica de la misma frecuencia que la frecuencia natural de vibración de la cuerda, y consta de los dos primeros armónicos. La frecuencia del primer componente es 200 Hz y la del segundo componente es 400 Hz. La amplitud de ambos componentes es la misma y está ajustada para que la amplitud máxima de la onda cuando quede resonando sea de 2 mm.
En el vídeo, que está ralentizado 400 veces respecto al movimiento real de nuestra cuerda, podemos observar cómo se superponen los dos primeros modos de vibración. Al entrar en resonancia por la acción del soporte, el movimiento de la cuerda va incrementando rápidamente su amplitud. Cuando el soporte se detiene, lo cual ocurre en el segundo 20 del vídeo o en el 50 ms de la realidad, y dado que no hemos tenido en cuenta ninguna fuerza de amortiguación, la amplitud de la onda permanece estable durante el resto del vídeo.
Vemos que el conjunto de la cuerda oscila arriba y abajo una vez cada 2 segundos, como corresponde a la frecuencia fundamental. Esto lo podemos ver mejor si nos fijamos en el punto central de la cuerda, el que está en 0,5 m: podemos apreciar en el vídeo que este punto oscila arriba y abajo haciendo un Movimiento Armónico Simple con la frecuencia del primer modo de resonancia de nuestra cuerda, que coincide con la frecuencia fundamental de la oscilación del soporte que está introduciendo la perturbación, es decir, 0,5 Hz en el vídeo o 200 Hz en la realidad.
Pero, a la vez, observamos que la cuerda se divide por el medio en dos partes iguales y que cada una de estas partes oscila, de forma complementaria una de la otra, a una frecuencia doble de la que tiene el conjunto de la cuerda, es decir, a 400 Hz en la realidad o a 1 Hz en el vídeo. Este movimiento es similar al que tendría la cuerda si solo se hubiera introducido en ella el segundo modo de resonancia y pivotara en torno al punto central (como en la figura 21). Pero este punto central en el modo segundo sería un nodo y, por lo tanto, permanecería inmóvil. La diferencia reside en que ahora este punto central oscila también arriba y abajo, en cuanto que es el punto de máxima amplitud, el vientre, del primer modo de resonancia.
En este caso sencillo en el que se combinan solamente los dos primeros modos de resonancia, nos resulta fácil apreciar que el movimiento total de la cuerda es el resultado de la composición de estos dos movimientos, pero a medida que el número de los componentes que vibran aumenta, la vibración de la cuerda se hace más y más compleja, hasta un punto en el que ya no es posible discernirlos ni siquiera en un vídeo ralentizado.
Por otra parte, hay que tener en cuenta que en nuestra simulación solamente hemos contemplado el caso de que la excitación que genera la onda sobre la cuerda se realice a través de uno de los extremos fijos de la cuerda. Pero la cuerda de un instrumento musical real puede ser excitada de múltiples maneras, bien por un golpe —tal como el que realiza el macillo en el piano—, bien al ser pulsada —como en el caso de la guitarra o del clavecín— o bien al ser frotada —como ocurre en el violín—. El lugar en el que se produce la excitación de la cuerda también es relevante para la sonoridad que se obtiene, pues, dependiendo de la posiciones en las que se produce el estímulo y de las intensidades de éste, se potenciarán o se atenuarán unos u otros modos de resonancia de la cuerda, con lo que se despertarán en mayor o menor medida unos u otros armónicos.
Veamos ahora un vídeo que simula de una forma más completa el movimiento de una cuerda real cuando produce un sonido armónico. En él se observa la vibración de nuestra cuerda cuando es excitada por una perturbación constituida por un conjunto numeroso de componentes, alguno de los cuales coinciden con sus modos de resonancia, mientras que otros están alejados. La cuerda amplifica solamente aquellas frecuencias que coinciden o están muy próximas a sus modos de resonancia y deja pasar sin amplificar aquellas otras que están alejadas. De esta manera, como las frecuencias naturales de la cuerda son armónicas, la vibración resultante será también armónica, dando lugar a una nota musical. La frecuencia de esta nota es de 200 Hz, la frecuencia fundamental que por naturaleza tiene la cuerda de nuestra simulación. A fin de facilitar la observación en el vídeo, he diseñado el movimiento del soporte para que la cuerda responda de forma significativa a los ocho primeros modos de resonancia y, además, para que los componentes de más frecuencia disminuyan progresivamente su amplitud.
Al principio del vídeo observamos una vibración de poca amplitud y más bien de carácter aleatorio, pero rápidamente va adquiriendo periodicidad y ganando en amplitud. Sucede simplemente que aquellos componentes que están presentes en la oscilación del soporte, pero que no corresponden a ningún modo de vibración natural de nuestra cuerda, no son amplificados, permaneciendo siempre en su bajo nivel inicial, mientras que los componentes que corresponden a las frecuencias naturales de la cuerda resuenan y son amplificados. El resultado es que la cuerda vibra de una manera compleja, como consecuencia de la combinación de sus modos naturales de vibración, pero de una forma periódica, con lo que produce una vibración armónica.
En efecto, el movimiento que observamos en el vídeo se aproxima bastante al que podría ser el movimiento de una cuerda real. Al ser el movimiento de la cuerda el resultado de múltiples modos de vibración, la apariencia que observamos es un movimiento complejo en el que es casi imposible reconocer individualmente cada uno de los modos de vibración. Aun con todo, podemos apreciar que se trata de una vibración armónica, como podemos reconocer si nos fijamos en la clara periodicidad que se manifiesta cuando el soporte queda ya inmóvil. Podemos fijarnos en que cada dos segundos se repite el mismo movimiento, lo que supone una frecuencia de 0,5 Hz, que multiplicado por las 400 veces que está ralentizado el vídeo, nos da los 200 Hz de frecuencia que hemos atribuido a nuestra cuerda.
Así pues, mediante este vídeo hemos podido hacernos una idea intuitiva de que una cuerda tensada selecciona de modo natural aquellas perturbaciones que coinciden con sus modos naturales de vibración, actuando como si se tratara de un filtro, de modo que, ante una perturbación compleja, reacciona positivamente y se acopla bien sólo en aquellas frecuencias que coinciden con sus modos naturales de vibración.
Conclusión
A lo largo de este módulo hemos estudiado que el sonido armónico o musical se produce cuando un cuerpo cuyos modos naturales de vibración son múltiplos enteros de una frecuencia fundamental es excitado por una fuerza vibratoria que contiene algunas de esas frecuencias o todas ellas, con las que entra en resonancia y se generan ondas estacionarias.
- Capítulo siguiente: Capítulo 9. Envolventes de amplitud y de frecuencia
- Capítulo anterior: Capítulo 7. El sonido armónico
2 comentarios:
Excelente material
Muchas gracias por tu comentario.
Publicar un comentario